
Любимый вопрос потенциального игрока: «Можно ли выиграть в казино?». На этот вопрос я отвечал неоднократно в той или иной форме в своих статьях. Если вдруг не читали, то напомню, что ответ такой: да, выиграть разово можно и довольно легко, а вот зарабатывать игрой (быть в плюсе на дистанции) от очень сложно до практически невозможно. Но иногда я встречаю «продвинутую» форму того же вопроса новичка, которая звучит так «Каковы шансы (вероятность) выиграть в казино?». При виде такого вопроса сразу вспоминаю бородатый анекдот: «Какова вероятность встретить на улице живого динозавра? - Пятьдесят процентов: может, встретишь, а может, и нет...» В общем виде, действительно, может, выиграешь, может, нет. Тем не менее, сейчас я хочу вполне серьёзно ответить на вопрос о шансах выигрыша в казино, причём не важно, оффлайн это казино или онлайн. Игры там практически одни и те же, так что и шансы на выигрыш при условии честной игры одинаковы. Предупреждаю только, что объяснение кому-то покажется слишком сложным (а кому-то примитивным), в крайнем случае, можно пропустить неинтересное и перейти к примерам и выводам в конце ;).
Можно ли сосчитать вероятность выиграть в казино? Да! Правда, сделать это не так просто. Ну для начала мы все понимаем, что казино - это набор очень разных азартных игр со своими правилами и характеристиками. Поэтому для каждой игры вероятность выиграть будет своя. Более того, если в игре возможны различные типы ставок или же принятие решений в процессе, то это также будет влиять на итоговую вероятность. А ещё ведь могут быть ставочные стратегии, они тоже изменят результат, по сравнению с игрой флэтбетом (одинаковыми ставками). В общем, переменных много, но их все при желании можно учесть.
В принципе, любая игра казино - это некий случайный процесс. Например, в рулетке - это случайное и равновероятное выпадение чисел от 1 до 37. В карточных играх - случайное выпадение последовательности карт. В игровых автоматах - выпадение символов на барабанах, ну и так далее. Ну а для нас, для игроков, будет другое случайное событие: денежный результаты игры. Мы можем проиграть деньги, вернуть ставку или её часть, а также выиграть некоторую сумму. Любой случайный процесс имеет две основополагающие характеристики: математическое ожидание (МО) и дисперсию или среднеквадратичное отклонение (СКО). Математическое ожидание (обозначается M или µ) по определению - это среднее значение случайной величины. Мы делаем ставку и случайным образом получаем выплаты, в нашем случае МО показывает, сколько мы в среднем выиграем или проиграем. Дисперсия (D) - мера разброса случайной величины, то есть её отклонения от математического ожидания. На практике для определения разброса чаще используют показатель среднеквадратического отклонения (СКО, обозначается σ - сигма), которое вычисляется как корень из дисперсии. В соответствии с центральной предельной теоремой теории вероятности сумма большого количества слабо зависимых случайных величин примерно одного масштаба имеет распределение близкое к нормальному. Наша игра в казино в целом удовлетворяет теореме: каждая раздача, спин практически независимы (небольшая зависимость может появляться только в карточных играх, если не перемешивать колоду), в итоге нашей игры они суммируются, и в большинстве случаев случайные величины, то есть выплаты, примерно одного масштаба (исключением тут могут быть слоты с крупными выигрышами, например, джекпотом). Итак, мы выяснили, что результаты игры в казино могут быть представлены при помощи нормального распределения случайной величины (оно же распределение Гаусса). Если у вас есть высшее образование, то из курса математики вы можете помнить, что кривая нормального распределения выглядит как колокол - его максимум соответствует матожиданию, а ширина, «расплющенность» зависит от СКО. Картинка ниже познакомит вас с видом графика плотности вероятности нормального распределения, а также его формулой (для общего развития, тут мы по ней непосредственно ничего считать не будем).
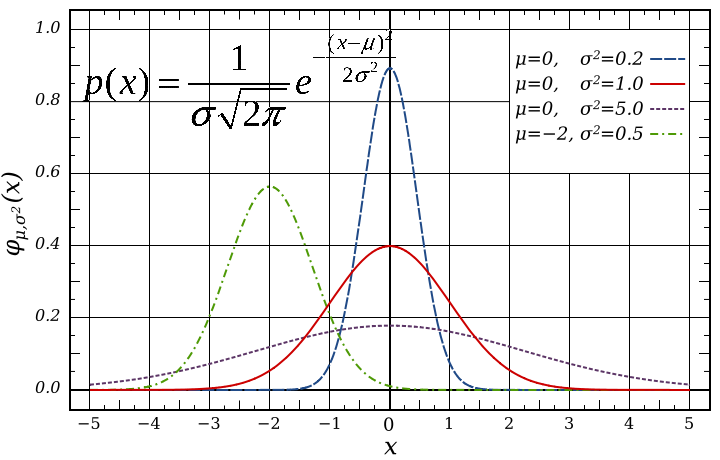
Графики выше можно интерпретировать как возможные результаты различных игр. По оси Х откладывается финансовый итог игры, а по оси Y - его вероятность (в данном случае на числа смотреть не надо, они даны для указанных образцовых случаев, а не реальных игр казино). У нас есть три игры с нулевым МО: синий график с низкой дисперсией будет ближе к игре на шансы в рулетке без зеро, красный график пошире - это может быть покерная игра, рулетка в число или слот с низкой дисперсией но нулевым МО, а самый широкий фиолетовый - слот с высокой дисперсией, и опять же нулевым МО. Правда, игры с нулевым МО в казино вы не найдёте, потому что они не приносят заведению прибыль. Исключение тут разве что казино BetVoyager, где все игры есть в «нулевых версиях», но там берут комиссию с выигрыша по итогам сессии. На практике все игры казино имеют такие правила, что матожидание для игрока будет отрицательным, результат мы видим на зелёном графике, это может быть блэкджек, например. Мы видим. что вероятность плюса или минуса для «нулевых» игр одинакова - графики симметричны относительно нуля. В нашу условную рулетку можно с небольшой вероятностью выиграть единицу, и с такой же вероятностью - проиграть. Выиграть двойку уже практически невероятно - дисперсия невелика, результаты будут ближе к нулю. А вот в условный покер уже можно выиграть или проиграть уже двойку, а в условных слотах можно сорвать даже большой куш - пятёрку, но можно столько же и проиграть. А вот в блэкджеке из-за отрицательного матожидания по этому графику быть в плюсе нам практически не светит. За ноль по оси Х заходит только маленький кусочек... На самом деле, не стоит пугаться, что в казино нельзя выиграть, конкретно этот график для блэкджека можно интерпретировать, как результат игры после десятка тысяч сдач. Если игр будет меньше, то график будет смещаться вправо ближе к нулю, а значит, шансы что-то выиграть будут расти.
Как же узнать, чему равно МО и СКО в конкретной игре? Во многих играх, таких как рулетка, их можно посчитать по формуле даже вручную. В более сложных, вроде блэкджека, покера или слотов их проще расчитать методом компьютерного моделирования. Для большинства игр эти величины посчитаны и известны, матожидание, в частности, я привожу в разделе «Стратегий» - это важнейшая характеристика любой игры для умного игрока. Данные по СКО менее доступны, просто потому, что кроме достаточно серьёзных игорных математиков они мало кого интересуют. Но зная эти два параметра мы можем рассчитать, какие результаты нас ждут. Точнее, найти вероятность того или иного исхода игры. Правда, нам надо сделать ещё один шаг - добавить в «уравнение» размер и количество ставок. Если мы играем флэтбетом, то на дистанции в n игр с величиной ставки S матожидание результата игры будет равно n*S*µ, а СКО - σ*S*√n. Для простоты лучше принять ставку равной единицы, дальше полученные числа можно подставлять в формулу, которую вы видите на картинке выше. Или проще, если у вас есть Excel в функцию НОРМ.РАСП. Если вы хотите узнать, какая вероятность остаться в плюсе (то есть те самые шансы на выигрыш, которые мы хотим найти), то берём 1-НОРМ.РАСП, подставляем в качестве аргумента X ноль, среднее и стандартное отклонение - наши МО и СКО, значение Интегральная указываем истина.
Давайте, наконец-то, посчитаем реальный пример. Мы играем в рулетку флэтбетом на шансы. Базовое матожидание нам давно известно, оно составляет -1/37 (в среднем игрок проигрывает 1/37 от каждой ставки) СКО для рулетки ещё можно посчитать по формулам, а можно найти в интернете, для ставок на шансы оно близко к единице - 0,9996. Предположим, что мы делаем 100 ставок, в этом случае МО=-100/37=-2,7, а СКО=корень(100)*0,9996=10. Подставляем в формулу: 1-НОРМ.РАСП(0;-100/37;10;ИСТИНА)=39%. А теперь сделаем скачок на 10 тыс. спинов, тут МО=-10000/37=-270, СКО=корень(10000)*0,9996=100, подставляем в формулу 1-НОРМ.РАСП(0;-10000/37;100;ИСТИНА)=0,35%. Да, шансы остаться в плюсе в рулетке после 10 тыс. спинов призрачны... Возможно, кто-то из вас слышал про «правило трёх сигм», так вот вероятность отклонения от матожидания на величину больше 3*σ составляет порядка 0,3%! У нас тут примерно такая ситуация и есть: чтобы выйти в плюс, надо иметь отклонение в 270 ставок, при σ=100 это лишь немногим меньше 3σ. Давайте посмотрим, как повлияет на нашу вероятность успеха изменение СКО. Возьмём ставки не на шансы, а в число. Даже на логическом уровне понятно, что дисперсия (разброс результатов) тут гораздо выше, чем при ставках на шансы. И действительно, СКО составляет 5,84, давайте сразу же посмотрим шансы остаться в плюсе: 1-НОРМ.РАСП(0;-10000/37;100*5,84;ИСТИНА)=32%. Здесь плюс достигается при величине меньше чем пол сигмы (270/584=0,46), поэтому и шансы немаленькие. Но это не значит, что игра на числа более выгодна - матожидание не изменилось, а большие шансы остаться в плюсе компенсируются большим риском крупно проиграться. Если в случае игры на шансы вероятность остаться в плюсе равная вероятности проиграть больше 540 ставок и равна 0,35%, то при игре на числа вероятность проиграть более 540 ставок (то есть 270 по МО и ещё 270 сверху) будет тоже 32%. Кстати, если вас интересует вероятность выиграть не менее определённой суммы, то указываем её в формуле вместо нуля. Например, вероятность выиграть 100 ставок, играя на числах равна 1-НОРМ.РАСП(100;-10000/37;100*5,84;ИСТИНА)=26%, не намного меньше, чем шансы просто выйти в ноль.
Если говорить о других играх, то наименьшая дисперсия у пай гоу покера, она составляет 0,75. При МО по оптимальной стратегии в районе -2,6% получается, что шансы остаться в плюсе на 10 тыс. сдач равны 1-НОРМ.РАСП(0;-10000*0,026;100*0,75;ИСТИНА)=0,02%. Как видите, шансы выиграть в пай гоу на большой дистанции микроскопические. Теперь посмотрим на фаворитов по матожиданию, например, в блэкджеке МО порядка -0,5%, а СКО 1,15 (числа могут немного отличаться в зависимости от варианта правил). На 10 тыс. сдач вы останетесь в плюсе в 1-НОРМ.РАСП(0;-10000*0,005;100*1,15;ИСТИНА)=33%. Неплохие шансы, тем более, что в отличие от рулетки в среднем вы ожидаете проигрыш лишь 50 ставок, а не 270. Ещё интереснее результаты у видеопокера. При практически том же матожидании в -0,46% (оптимальная стратегия в валетах и выше с полной оплатой) СКО изрядно выше - 4,42. Получается, шансы остаться в плюсе: 1-НОРМ.РАСП(0;-10000*0,0046;100*4,42;ИСТИНА)=46%. Почти в половине случаев, даже на столько длинной дистанции, игрок в видеопокер может остаться в плюсе. В случае рулетки мы видели, как дистанция и дисперсия (СКО) влияет на вероятность остаться в выигрыше. Давайте посмотрим, насколько важно матожидание. Предположим, что вместо видеопокера мы играем в слот с точно таким же СКО (это будет автомат с дисперсией пониже средней). Возьмём для нашего слота МО в -4%, у большинства игровых автоматов в онлайне этот показатель лежит в диапазоне 3-5% (у слотов с джекпотом обычно хуже). Получаем вероятность выигрыша на 10000 спинов: 1-НОРМ.РАСП(0;-10000*0,04;100*4,42;ИСТИНА)=18%. Как видим, довольно высокая дисперсия оставляет и тут неплохие шансы на плюс, но они в 2,5 раза меньше, чем у видеопокера с высоким МО.
Итак, мы знаем, как посчитать шансы на выигрыш на определённой дистанции при игре одинаковыми ставками. МО и СКО для основных игр можно найти в интернете, единственное, у вас будут проблемы со слотами: если МО для некоторых слотов публикуются, то СКО обычно не раскрывается, максимум «по ощущениям» указывают низкую, среднюю или высокую дисперсию. А вот если вы используете какую-то ставочную стратегию, что ручной расчёт уже будет проблематичен. Тут вам поможет только компьютерная симуляция. Есть старенькая программа, которую я уже упоминал на сайте - Gambler Odds (её сайт закрылся, так что даю прямую ссылку на скачивание). Она строит графики, в том числе вероятность выигрыша (как и вероятность банкротства) для нескольких игр, а также различных ставочных стратегий, в том числе вы можете добавить свою ставочную стратегию и даже свою игру. Ниже вы можете видеть пример работы этой программы для «монетки», рулетки флэтбетом на шансы и числа, а также мартингейла на рулетке.
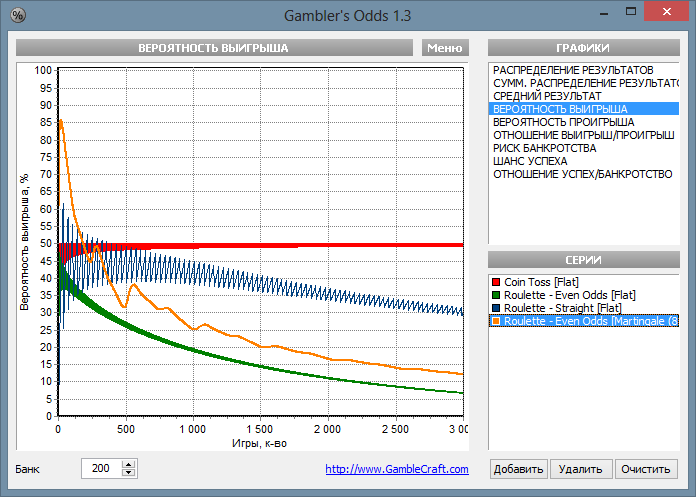
Как видите, мартингейл на первых десятках спинов даёт очень немаленькие шансы на выигрыш, но уже после пары сотен они не поднимаются выше 50%, а дальше падают ниже, чем у ставок в число и постепенно приближаются к графику флэтбета на шансы. Только не надо, глядя на этот график, делать выводы о том, что можно играть в плюс по мартингейлу, если делать сессии по 20 спинов. Пусть вероятность выиграть при этом составляет 85%, но выиграете вы за это время меньше 10 ставок. Зато в 15% случаев попадёте в минусовую волну, и проигрыш может составить более 100 ставок! На самом деле, все сыгранные вами сессии, с точки зрения математики, суммируются, и через 50 сессий по 20 ставок вы окажетесь там, где стоит цифра 1000 игр, а вероятность быть в плюсе при игре мартингейлом составляет лишь 25%. Рекомендую побаловаться с этой программой, можете потестировать ваши ставочные стратегии в рулетке и сравнить их шансы на успех с игрой флэтбетом.
В общем, теперь вы знаете, каковы реальные шансы выиграть в казино и даже можете сами их посчитать или хотя бы посмотреть компьютерный анализ. К сожалению, чем больше вы играете, тем эти шансы меньше. Но выбирая игру с большими МО и СКО, вы эти шансы увеличиваете. Правда, имейте в виду, что дисперсия - меч обоюдоострый: у вас больше шансы остаться в плюсе, но при этом больше вероятность и крупно проиграться. Остаётся только пожелать играть мудро и не без везения!
Автор: Шероков Юрий. Ваш покорный слуга, также автор большей части сайта «Казино Онлайн» ;).


